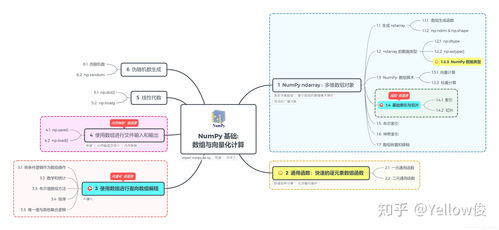
在编程的世界里,数据科学和机器学习逐渐成为热门领域,而NumPy作为Python中的一个基础库,无疑是每一位开发者绕不开的话题。今天,让我们跟随一位热爱技术的小白——小明,一起走进NumPy的世界,从零开始探索它的奥秘。
为什么选择NumPy?
小明最初接触NumPy是因为听说它是处理大规模数值计算的强大工具。作为一名对数据分析感兴趣的程序员,他深知高效的数据操作对于项目的重要性。于是,他决定深入研究这个库,并记录下自己的学习心得。
NumPy的核心概念
在学习的过程中,小明发现NumPy最核心的概念是数组(ndarray)。与Python原生列表不同的是,NumPy数组具有固定的数据类型和维度,这使得它在处理大型数据集时更加高效。例如,创建一个简单的NumPy数组:
import numpy as np
arr = np.array([1, 2, 3, 4])
print(arr)通过这段代码,小明轻松生成了一个一维数组。他进一步了解到,NumPy还支持多维数组的创建,比如二维数组:
matrix = np.array([[1, 2], [3, 4]])
print(matrix)这些基本操作让小明对NumPy有了初步的认识。
广播机制的魅力
随着学习的深入,小明遇到了一个有趣的功能——广播机制(Broadcasting)。这一机制允许不同形状的数组之间进行算术运算,只要满足一定的规则。例如,当一个数组的某一维度为1时,NumPy会自动扩展该维度以完成运算。小明用以下代码验证了这一点:
a = np.array([[1], [2], [3]])
b = np.array([4, 5, 6])
result = a + b
print(result)运行结果表明,即使a是一个列向量,b是一个行向量,它们仍然可以相加,最终得到一个矩阵。这种灵活性让小明对NumPy的广播机制赞不绝口。
精度控制的艺术
在实际应用中,小明发现有时需要对浮点数进行精确比较。然而,由于计算机存储浮点数的方式,直接使用等号判断可能会导致意外的结果。这时,NumPy提供的np.allclose函数就显得尤为重要。它可以用来判断两个数组是否“接近”相等,而不是完全相等。例如:
np.allclose(1e-9, 2e-9) # 默认情况下返回True
np.allclose(1e-9, 2e-9, atol=1e-17) # 指定更严格的容忍度,返回False通过调整参数atol(绝对容差)和rtol(相对容差),小明能够根据具体需求灵活控制比较的精度。
总结与展望
经过一段时间的学习,小明对NumPy的理解逐渐加深。他意识到,NumPy不仅是一个强大的数值计算工具,更是通往数据科学领域的桥梁。在未来,他计划继续探索NumPy的高级功能,如线性代数运算、傅里叶变换等,为自己的技能树添砖加瓦。
如果你也是一名对数据科学充满热情的开发者,不妨跟随小明的脚步,开启属于你的NumPy之旅吧!



发表评论 取消回复