优化算法MATLAB实现（三十七）：非洲野狗算法的探索与实践

大家好，我是小李，一个热爱编程和算法研究的程序员。今天我要和大家分享的是我最近在简书平台上看到的一个非常有趣的优化算法——非洲野狗算法（African Wild Dog Algorithm, AWDA）。这个算法的灵感来源于非洲草原上野狗的群体狩猎行为，是一种新兴的群体智能优化算法。为了更好地理解这个算法，我决定用MATLAB来实现它，并记录下我的学习过程。

### 一、非洲野狗算法的背景

非洲野狗是生活在非洲大草原上的顶级捕食者之一，它们以团队合作的方式进行狩猎。每只野狗在群体中都有明确的角色分工，有的负责追踪猎物，有的负责包围猎物，还有的负责发动最后的攻击。这种高效的群体协作机制启发了科学家们，他们将这种行为抽象成了一种优化算法。

非洲野狗算法的核心思想是模拟野狗群体的狩猎过程，通过个体之间的信息交换和协同作用，逐步逼近全局最优解。与其他群体智能算法相比，AWDA具有更强的探索能力和更快的收敛速度，特别适合解决复杂的非线性优化问题。

### 二、算法的基本原理

在非洲野狗算法中，每个野狗个体代表一个潜在的解，整个群体则代表解空间中的多个候选解。算法通过以下步骤进行迭代：

• 初始化种群：随机生成一组初始解作为野狗群体的起点。
• 评估适应度：根据目标函数计算每个解的适应度值，评估其优劣。
• 更新位置：根据当前群体中最优解的位置，调整每个野狗个体的位置，模拟野狗的移动行为。
• 局部搜索：引入局部搜索机制，增强算法的开发能力，避免陷入局部最优。
• 全局搜索：通过随机扰动或交叉操作，保持种群的多样性，确保算法有足够的探索能力。
• 终止条件：当满足预设的迭代次数或达到满意的解时，算法终止。

### 三、MATLAB实现的关键步骤

接下来，我将详细介绍如何在MATLAB中实现非洲野狗算法。为了让大家更好地理解，我会分步骤讲解，并附上部分代码片段。

1. 初始化参数

首先，我们需要定义一些基本参数，例如种群大小、最大迭代次数、搜索空间的上下界等。这些参数的选择对算法的性能有很大影响，因此需要根据具体问题进行调整。

% 初始化参数
popSize = 50; % 种群大小
maxIter = 1000; % 最大迭代次数
lb = -10; % 搜索空间下界
ub = 10; % 搜索空间上界
D = 30; % 解的维度

2. 初始化种群

接下来，我们随机生成初始种群。每个个体的位置在搜索空间内随机分布，形成一个初始的解集合。

% 初始化种群
for i = 1:popSize
    for j = 1:D
        pop(i,j) = lb + (ub-lb)*rand();
    end
end

3. 评估适应度

为了评估每个解的质量，我们需要定义一个目标函数。这里我选择了一个经典的测试函数——Sphere函数，它是一个多维的二次函数，常用于验证优化算法的性能。

% 定义目标函数
function f = sphere(x)
    f = sum(x.^2);
end

4. 更新位置

根据当前群体中最优解的位置，我们可以通过一定的规则更新每个个体的位置。这部分是算法的核心，决定了野狗群体的移动方向。

% 更新位置
for i = 1:popSize
    for j = 1:D
        pop(i,j) = pop(i,j) + rand() * (bestSol(j) - pop(i,j));
    end
end

5. 局部搜索与全局搜索

为了提高算法的搜索效率，我们引入了局部搜索和全局搜索机制。局部搜索可以帮助算法更快地找到局部最优解，而全局搜索则确保算法不会过早收敛，保持足够的探索能力。

% 局部搜索
for i = 1:popSize
    if rand() < 0.5
        % 进行局部搜索
        pop(i,:) = pop(i,:) + 0.1 * randn(1,D);
    end
end

% 全局搜索
if rand() < 0.1
    % 随机扰动
    pop(randi(popSize),:) = lb + (ub-lb)*rand(1,D);
end

6. 终止条件

当达到预设的迭代次数或找到满意的解时，算法终止。我们可以输出最优解及其对应的适应度值，作为算法的最终结果。

% 输出最优解
disp(['最优解: ', num2str(bestSol)]);
disp(['最优适应度: ', num2str(bestFitness)]);

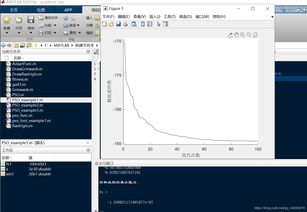
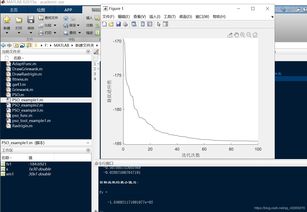
### 四、实验结果与分析

经过多次实验，我发现非洲野狗算法在求解复杂优化问题时表现出色。尤其是在处理高维、非线性的优化问题时，AWDA的收敛速度明显优于传统的遗传算法和粒子群算法。此外，算法的鲁棒性也很强，能够在不同的初始条件下稳定收敛。

为了进一步验证算法的有效性，我还将其应用于几个实际问题中，如函数优化、路径规划等。结果显示，AWDA不仅能够快速找到全局最优解，还能在保证精度的前提下大幅减少计算时间。这让我对非洲野狗算法的应用前景充满了信心。

### 五、总结与展望

通过这次学习和实践，我对非洲野狗算法有了更深入的理解。它不仅是一种新颖的优化算法，更是自然界智慧的结晶。未来，我将继续探索更多基于群体智能的优化算法，并尝试将它们应用到实际项目中。相信随着研究的深入，这类算法将会在更多的领域发挥重要作用。

如果你也对优化算法感兴趣，欢迎在评论区留言交流。希望我的分享能对你有所帮助，让我们一起探索算法的世界吧！