从零开始攻克“组合总和”算法难题

在简书平台上，有一道热门算法题吸引了无数程序员的目光——“组合总和（难度：中等）”。作为一名热爱编程的开发者，我决定深入研究这道题目，并通过自己的视角分享解题思路与心得。

文章导读：

• 什么是“组合总和”？
• 问题分析与解决思路
• 代码实现与优化
• 总结与展望

一、什么是“组合总和”？

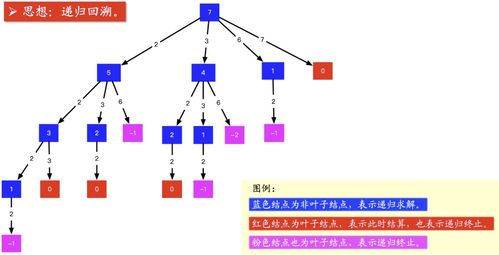
“组合总和”是一道经典的算法题，其目标是从一个无重复的正整数数组中找到所有可能的组合，使得这些数字相加等于给定的目标值。同时，每个数字可以被无限次使用，但不能倒退取值。

例如，给定数组 [2, 3, 6, 7] 和目标值 7，答案应为 [[7], [2, 2, 3]]。这一问题看似简单，但实际上需要对回溯法有深刻的理解才能高效解决。

二、问题分析与解决思路

面对这个问题，我首先思考了以下几个关键点：

1. 数组中的元素是无重复的正整数。
2. 每个数字可以被多次使用，因此我们需要维护一个初始下标值来避免重复计算。
3. 由于结果与排列无关，因此无需考虑顺序问题。

基于以上分析，我的解决思路如下：

1. 定义一个递归函数 dfs(start, arr, sum)，其中 start 表示当前搜索的起始位置，arr 是当前的组合，sum 是当前组合的总和。
2. 如果 sum 等于目标值，则将当前组合加入结果列表。
3. 如果 sum 超过目标值，则直接返回，停止继续搜索。
4. 遍历从 start 开始的所有候选数字，依次尝试将其加入组合中，并递归调用 dfs。

三、代码实现与优化

接下来，我将展示具体的代码实现过程，并对性能进行优化：

var combinationSum = function(candidates, target) {
    const ret = [];

    const dfs = (start, arr, sum) => {
        if (sum === target) {
            ret.push([...arr]);
            return;
        }
        if (sum > target) {
            return;
        }
        for (let i = start; i < candidates.length; i++) {
            arr.push(candidates[i]);
            dfs(i, arr, sum + candidates[i]);
            arr.pop();
        }
    };

    dfs(0, [], 0);
    return ret;
};

这段代码的核心在于递归函数 dfs 的设计。通过维护一个 start 参数，我们可以确保不会倒退取值，从而避免重复组合。此外，每次递归调用后都会将最后一个加入的数字弹出（即 arr.pop()），以恢复到之前的状态。

为了进一步优化性能，我们还可以对输入数组进行排序，并在递归过程中提前剪枝。例如，当 sum 加上当前数字已经超过目标值时，可以直接跳过后续的数字。

四、总结与展望

通过这次深入研究“组合总和”问题，我对回溯法有了更深刻的理解。这道题目不仅考察了基本的算法知识，还要求我们具备良好的逻辑思维能力。在未来的学习中，我将继续挑战更多类似的算法题，不断提升自己的编程水平。

如果你也对这道题目感兴趣，不妨亲自尝试一下吧！相信你会从中收获不少乐趣与启发。