集合图与韦恩图的区别：从初学者到精通

作为一个对数学和逻辑充满兴趣的人，我一直对集合图和韦恩图这两个概念感到困惑。它们看起来如此相似，却又有着微妙的差异。今天，我想和大家分享一下我在这段时间里对这两者的理解和探索，希望能帮助那些同样在学习这些概念的朋友。

首先，让我们从集合图说起。集合图是一种用于表示集合及其关系的图形工具。它可以帮助我们直观地理解集合之间的交集、并集、补集等操作。集合图的形式多种多样，最常见的就是用圆圈或椭圆来表示集合，而集合中的元素则用点或符号表示。

例如，假设我们有两个集合A和B，A包含{1, 2, 3}，B包含{2, 4, 6}。我们可以用两个相交的圆圈来表示这两个集合，其中交集部分表示的是同时属于A和B的元素，即{2}。通过这种方式，我们可以非常直观地看到集合之间的关系。

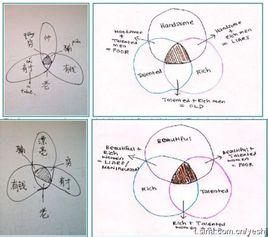
接下来，我们来看看韦恩图。韦恩图其实是一种特殊的集合图，由英国数学家约翰·韦恩（John Venn）于1880年提出。它的主要特点是使用封闭的曲线（通常是圆形或椭圆形）来表示集合，并且这些曲线可以相互重叠，以表示集合之间的交集。

与一般的集合图不同，韦恩图不仅限于两个集合，它可以扩展到三个、四个甚至更多个集合。每个集合都用一个封闭的曲线表示，而这些曲线的重叠部分则表示多个集合的交集。韦恩图的最大优势在于它能够清晰地展示多个集合之间的复杂关系，尤其是在处理多个集合的交集、并集和补集时。

举个例子，如果我们有三个集合A、B和C，A包含{1, 2, 3}，B包含{2, 4, 6}，C包含{3, 5, 7}。那么在韦恩图中，这三个集合的交集部分将表示同时属于A、B和C的元素，即空集（因为没有元素同时属于这三个集合）。而A和B的交集是{2}，A和C的交集是{3}，B和C的交集是空集。

现在，我们已经了解了集合图和韦恩图的基本概念，那么它们之间到底有什么区别呢？其实，两者的区别主要体现在以下几个方面：

1. 适用范围： 集合图是一个更广泛的概念，它可以用来表示任何类型的集合及其关系。而韦恩图则是一种特定的集合图，主要用于展示多个集合之间的交集、并集和补集。


2. 图形表示： 集合图的形式较为灵活，可以根据需要选择不同的图形来表示集合，如矩形、圆形、椭圆形等。而韦恩图通常只使用封闭的曲线（如圆形或椭圆形）来表示集合，并且这些曲线必须是封闭的。


3. 复杂度： 韦恩图更适合用于展示多个集合之间的复杂关系，尤其是在处理多个集合的交集、并集和补集时。而集合图则更加通用，适用于各种场景，包括简单的集合关系和复杂的逻辑运算。


4. 应用场景： 韦恩图常用于数学、逻辑学、统计学等领域，特别是在处理多个集合之间的关系时。而集合图则更广泛地应用于计算机科学、数据结构、数据库等领域，尤其是在描述数据之间的关系时。

在学习集合图和韦恩图的过程中，我发现它们不仅仅是一些抽象的数学概念，而是可以在实际生活中找到很多应用场景。比如，在数据分析中，我们经常需要处理多个数据集之间的交集、并集和补集。这时，韦恩图就成为了一个非常有用的工具，可以帮助我们快速理解数据之间的关系。

此外，在编程中，集合的操作也是非常常见的。无论是Python中的集合类型，还是SQL中的集合查询，集合图和韦恩图都能帮助我们更好地理解和设计算法。例如，在编写一个程序时，我们需要判断某个元素是否同时属于多个集合，或者计算多个集合的交集和并集。这时，韦恩图可以帮助我们更直观地理解问题，并找到最优的解决方案。

最后，我还发现，集合图和韦恩图在教育领域也有着广泛的应用。无论是小学的数学课，还是大学的离散数学课程，集合图和韦恩图都是教学中不可或缺的工具。通过这些图形工具，学生可以更轻松地理解集合的概念，掌握集合之间的关系。

通过对集合图和韦恩图的深入学习，我逐渐明白了它们之间的区别和联系。集合图是一个更广泛的概念，适用于各种场景，而韦恩图则是一种特殊的集合图，主要用于展示多个集合之间的复杂关系。无论是数学、逻辑学、数据分析，还是编程和教育，集合图和韦恩图都有着重要的应用价值。

未来，我希望能够继续深入研究这些概念，并将其应用到更多的实际场景中。我相信，随着我对这些概念的理解不断加深，我将能够在更多的领域中发现它们的价值。如果你也对集合图和韦恩图感兴趣，不妨一起探讨，分享你的见解和经验吧！