探索最长回文子串：从困惑到突破的编程之旅

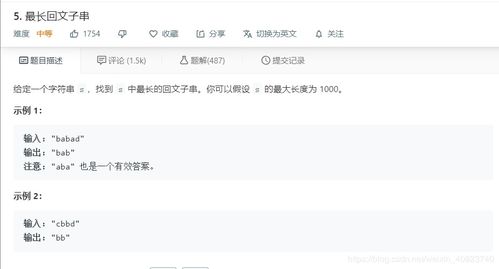
在简书平台上，最近有一个话题引起了我的极大兴趣——“最长回文子串”。作为一个热爱编程的开发者，我自然不会错过这个机会。今天，我想和大家分享一下我在这段学习过程中的心路历程，以及我是如何从最初的困惑一步步走到最终的突破。

一、初识回文子串

什么是回文子串？简单来说，回文是指一个字符串从左往右读和从右往左读是完全相同的。例如，“level”和“racecar”就是典型的回文。而回文子串则是指在一个给定的字符串中找到最长的回文子串。这个问题看似简单，但当我真正开始思考时，才发现它并不像表面看起来那么容易。

最初，我尝试用最直观的方法来解决这个问题：暴力枚举。即遍历所有可能的子串，然后逐一检查它们是否是回文。这种方法虽然能解决问题，但效率极低，时间复杂度高达O(n^3)，对于较长的字符串根本无法接受。我意识到，必须寻找更高效的算法。

二、动态规划的启示

在深入研究后，我发现动态规划（Dynamic Programming, DP）是一个非常有效的工具。动态规划的核心思想是通过将问题分解为更小的子问题，并利用这些子问题的解来构建最终的解决方案。具体到最长回文子串问题，我们可以用一个二维数组dp[i][j]来表示从索引i到j的子串是否是回文。

初始化时，单个字符显然是回文，因此dp[i][i] = true。接下来，我们需要考虑长度为2的子串，如果两个字符相同，则dp[i][i+1] = true。对于更长的子串，我们可以通过递推公式来判断：如果s[i] == s[j]且dp[i+1][j-1]为true，则dp[i][j]也为true。这样，我们就可以逐步构建出整个dp表。

然而，动态规划虽然提高了效率，但空间复杂度依然较高，尤其是当字符串长度较大时，内存消耗会成为一个问题。我开始思考，是否还有更优的解法？

三、中心扩展法的突破

经过一番探索，我发现了另一种更为巧妙的方法——中心扩展法。这种方法的核心思想是从每个字符（或字符对）为中心，向两边扩展，直到遇到不满足回文条件的情况为止。相比于动态规划，中心扩展法的时间复杂度为O(n^2)，但它的空间复杂度仅为O(1)，大大节省了内存。

具体实现时，我们需要考虑两种情况：奇数长度的回文（如“aba”）和偶数长度的回文（如“abba”）。对于奇数长度的回文，我们以单个字符为中心；对于偶数长度的回文，我们以两个相邻字符为中心。通过遍历字符串的每个字符（或字符对），并进行中心扩展，我们可以找到最长的回文子串。

为了验证这种方法的有效性，我编写了一个简单的Python代码来实现中心扩展法：

def longest_palindrome(s: str) -> str:
    if not s:
        return ""
    start, end = 0, 0
    for i in range(len(s)):
        len1 = expand_around_center(s, i, i)
        len2 = expand_around_center(s, i, i + 1)
        max_len = max(len1, len2)
        if max_len > end - start:
            start = i - (max_len - 1) // 2
            end = i + max_len // 2
    return s[start:end + 1]

def expand_around_center(s: str, left: int, right: int) -> int:
    while left >= 0 and right < len(s) and s[left] == s[right]:
        left -= 1
        right += 1
    return right - left - 1

四、总结与反思

通过这次对“最长回文子串”问题的探索，我不仅学到了新的算法技巧，更重要的是，我深刻体会到了编程的魅力。编程不仅仅是写代码，更是一种思维方式。面对复杂的问题时，我们需要不断尝试不同的方法，从多个角度去思考，才能找到最优的解决方案。

在这个过程中，我也意识到，编程的学习没有捷径可走。每一次的困惑和挫折，都是成长的机会。正是这些挑战让我更加坚定了继续前行的决心。未来，我将继续探索更多的算法和数据结构，不断提升自己的编程能力。

如果你也对编程感兴趣，不妨一起来探讨这个问题吧！相信你会在这个过程中收获很多。无论是动态规划还是中心扩展法，都只是编程世界中的冰山一角。让我们一起在编程的海洋中畅游，发现更多有趣的问题和解决方案。