揭秘：为什么银行存款和河流长度的首位数字更偏爱“1”？

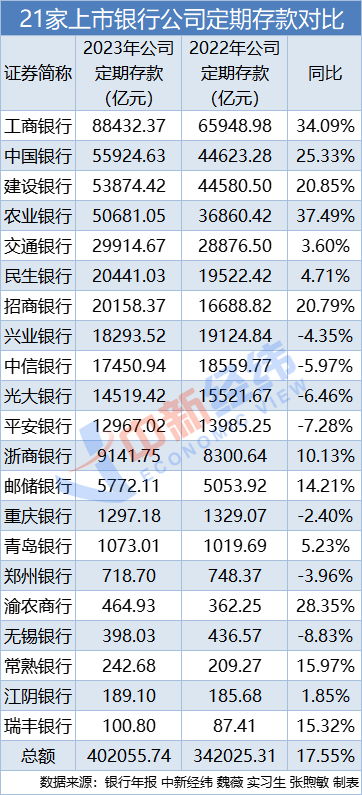
在知乎上，有一个看似简单却充满玄机的问题引发了热议——为什么银行存款、河流长度等数据的首位数字更容易出现“1”，而不是“9”？这个问题乍一听让人摸不着头脑，但深入探讨后才发现，这背后隐藏着一个令人惊叹的数学规律。

什么是本福特定律？
本福特定律的应用场景
生活中的例子
背后的逻辑是什么？

一、什么是本福特定律？

这位网友偶然间发现，无论是银行账户余额还是河流长度，首位数字为“1”的概率远高于其他数字。这种现象并非偶然，而是遵循了一条名为“本福特定律”的数学规律。该定律指出，在许多真实世界的数据集中，首位数字并不是均匀分布的，而是呈现出一种递减趋势。具体来说，“1”作为首位数字的概率约为30%，而“9”仅为不到5%。

这条定律最早由加拿大物理学家西蒙·纽科姆于1881年提出，并在20世纪被美国工程师弗兰克·本福特重新发现并推广，因此得名。

二、本福特定律的应用场景

那么，这个看似抽象的定律在生活中究竟有何意义呢？实际上，它已经被广泛应用于多个领域：

• 金融审计：税务部门利用本福特定律检测企业财务报表是否存在造假行为。如果某公司的账目数据不符合这一分布规律，就可能存在问题。
• 选举监督：尽管不能直接用于政治话题，但在某些统计分析中，人们会用本福特定律检查投票数据是否异常。
• 科学研究：从天文学到生物学，科学家们发现许多自然现象的数据也符合本福特定律。

三、生活中的例子

为了让读者更好地理解这一现象，我们不妨来看几个贴近生活的实例。

1. 银行存款：假设你观察了身边朋友的银行账户余额，你会发现大部分人的余额以“1”开头，比如1万元、1.5万元等，而以“9”开头的则很少见。
2. 河流长度：世界上著名河流的长度同样符合这一规律。例如，尼罗河全长约6650公里，首位数字是“6”，而亚马逊河全长约6992公里，首位数字是“6”。这样的分布完全符合本福特定律。
3. 人口统计数据：全球各国的人口数量也表现出类似的特征，首位数字为“1”的国家占很大比例。

四、背后的逻辑是什么？

为什么会存在这样的规律？其实，这与数据的增长方式密切相关。大多数现实世界的数据并非随机生成，而是经过长时间积累形成的。例如，一个人的银行存款通常是从零开始逐渐增加的。当余额从1万元增长到2万元时，需要翻倍；但从8万元增长到9万元时，只需增加12.5%。因此，以“1”开头的阶段持续时间更长，出现的概率自然更高。

此外，本福特定律还与对数分布有关。通过对数坐标系可以直观地看到，每个区间（如[1,2)、[2,3)……）所占的比例并不相等，而是呈递减趋势。

总结一下，本福特定律揭示了一个隐藏在日常生活中的奇妙规律。无论是在金融、科学还是其他领域，它都为我们提供了一种全新的视角去理解和分析数据。下次当你查看自己的银行账户或地图上的河流长度时，不妨留意一下这些数字的首位数字，说不定你会发现更多有趣的秘密！