深入解析：为什么softmax函数输出值可以作为概率预估？

引言

在机器学习和深度学习领域，softmax函数是一个不可或缺的组件，尤其是在处理多分类问题时。它能够将一个实数向量转换为一个概率分布，使得输出值可以作为概率预估。本文将深入探讨softmax函数的工作原理及其为何能够作为概率预估的原因。

什么是softmax函数？

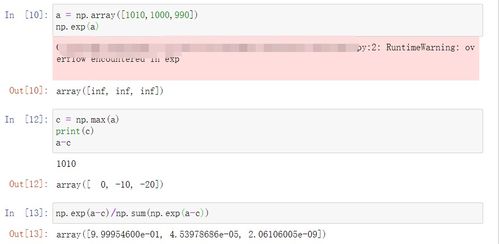
softmax函数，也称为归一化指数函数，是一种将实数向量转换为概率分布的函数。其数学表达式为：

softmax(z) = e^z / Σ(e^z_i)

其中，z是一个实数向量，Σ表示对所有元素求和，z_i是向量中的第i个元素。

softmax函数的特点

1. 输出值在0到1之间：由于指数函数的性质，softmax函数的输出值总是在0到1之间，这使得它能够表示概率。

2. 输出值之和为1：softmax函数的输出值之和总是等于1，这符合概率分布的基本性质。

3. 对数似然函数的导数易于计算：在训练过程中，我们通常使用交叉熵损失函数，而softmax函数与交叉熵损失函数的组合使得梯度计算变得简单。

为什么softmax函数输出值可以作为概率预估？

1. 概率分布的性质：如前所述，softmax函数的输出值满足概率分布的基本性质，即非负性和归一化。这使得它能够表示一个概率分布。

2. 多分类问题中的适用性：在多分类问题中，我们需要预测一个样本属于多个类别的概率。softmax函数能够将一个实数向量转换为一个概率分布，使得每个类别都有一个对应的输出值。

3. 梯度计算的便利性：在训练过程中，我们需要计算损失函数的梯度。softmax函数与交叉熵损失函数的组合使得梯度计算变得简单，这有助于模型的快速收敛。

softmax函数的应用

softmax函数在机器学习和深度学习领域有着广泛的应用，例如：

• 多分类问题：在多分类问题中，softmax函数用于将模型的输出转换为概率分布，从而进行类别预测。
• 语言模型：在自然语言处理领域，softmax函数常用于语言模型中，用于预测下一个词的概率分布。
• 神经网络的最后一层：在神经网络中，softmax函数通常作为最后一层，用于输出类别概率。

总结

softmax函数之所以能够作为概率预估，是因为它满足概率分布的基本性质，并且在多分类问题中具有很好的适用性。同时，它与交叉熵损失函数的组合使得梯度计算变得简单，有助于模型的快速收敛。

在实际应用中，我们需要根据具体问题选择合适的模型和损失函数。softmax函数作为一种常用的激活函数，为我们提供了一种有效的解决方案。