
一、初识直角椭圆
小李是一位热爱数学的学生,最近他在简书上看到了一道关于“直角椭圆”的中考压轴题。这道题目新颖且复杂,让小李感到既兴奋又困惑。所谓“直角椭圆”,是指在平面直角坐标系中,以某点为中心构造出一种特殊的椭圆图形,其特殊性在于它满足某些特定的几何条件。
例如,题目可能会要求椭圆上的任意一点到两焦点的距离之和为定值,同时还要满足直角三角形的性质。
小李意识到,这种题目不仅考察了对椭圆基本概念的理解,还融合了几何、代数等多方面的知识。
二、探索解题思路
面对这样一道复杂的题目,小李并没有轻易放弃。他开始回顾课本中关于椭圆的基本公式:c² = a² - b²以及x²/a² + y²/b² = 1。同时,他还查阅了一些课外资料,试图找到更多相关的解题技巧。
通过分析,小李发现,这类题目通常需要从以下几个方面入手:
- 确定椭圆的中心点及其参数
- 结合已知条件列出方程组
- 利用几何关系进行验证
在这个过程中,小李逐渐摸索出了属于自己的解题方法。
三、实战演练
为了检验自己的学习成果,小李决定尝试解答一道类似的题目。题目如下:
已知椭圆的两个焦点分别为F₁(0, -3)和F₂(0, 3),椭圆上的一点P满足∠PF₁F₂为直角,求该椭圆的标准方程。
经过一番思考,小李列出了以下步骤:
- 根据焦点位置判断椭圆的中心在原点,并设其标准方程为
x²/a² + y²/b² = 1。 - 由直角三角形的性质得出
|PF₁|² + |PF₂|² = |F₁F₂|²。 - 代入具体数据计算得到
a² = 18,b² = 9。 - 最终得出椭圆的标准方程为
x²/18 + y²/9 = 1。
通过这道题目的练习,小李更加深刻地理解了直角椭圆的解题思路。
四、总结与感悟
回顾整个解题过程,小李感慨良多。他认为,解决这类题目最重要的是耐心和逻辑思维能力。同时,他也意识到,数学的学习不仅仅是为了应付考试,更是一种提升自身思维能力的过程。
对于即将参加中考的同学,小李给出了几点建议:
- 熟练掌握基础知识,尤其是椭圆的相关公式。
- 注重几何与代数的结合,灵活运用各种解题方法。
- 多做练习,积累经验,提高应试能力。
最后,小李表示,虽然这道题目看似困难,但只要用心去研究,就一定能够找到答案。
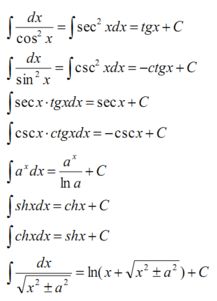


发表评论 取消回复