堆排序算法的深入解析与代码实践

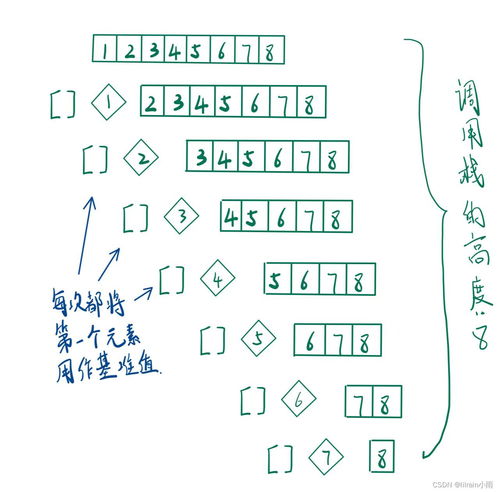
在编程的世界里，小李最近对堆排序算法产生了浓厚的兴趣。他发现这种算法不仅高效而且非常实用，于是决定深入研究一番，并分享他的学习心得。

堆排序是一种基于二叉堆数据结构的选择排序算法。它的主要思想是将待排序的序列构造成一个大顶堆或小顶堆，使得堆顶元素总是当前集合中的最大值或最小值。通过不断移除堆顶元素并重新调整堆结构，最终可以实现整个序列的有序排列。

小李总结了堆排序的几个核心步骤：首先，构建初始堆；其次，将堆顶的最大值取出放到序列末尾；最后，重新调整剩余元素构成新的堆，重复上述过程直到所有元素都完成排序。

为了更好地理解堆排序，小李动手编写了一段Python代码：

def heapify(arr, n, i):
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2
    if left < n and arr[i] < arr[left]:
        largest = left
    if right < n and arr[largest] < arr[right]:
        largest = right
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heapSort(arr):
    n = len(arr)
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)
    for i in range(n-1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]
        heapify(arr, i, 0)

这段代码清晰地展示了堆排序的实现过程，包括heapify函数和heapSort函数的定义。小李通过调试和运行这段代码，进一步加深了对堆排序的理解。

堆排序的时间复杂度为O(nlogn)，空间复杂度为O(1)。相比其他排序算法，堆排序具有较高的效率和稳定性，尤其适合处理大规模数据集。小李在实验中发现，当数据量较大时，堆排序的表现尤为突出。

除了理论上的学习，小李还尝试将堆排序应用到实际问题中。例如，在处理一组学生的考试成绩时，使用堆排序可以快速找到最高分和最低分，从而帮助老师更好地了解学生的学习情况。

总之，堆排序是一种强大且灵活的排序算法，值得每一位程序员深入学习和掌握。小李希望通过这篇文章，能够让更多的人了解堆排序的魅力，并激发大家对算法学习的热情。