在简书平台上,有一个关于数学的热搜话题——“探索勾股数组”,这激发了小明(化名)对这一古老数学问题的兴趣。他开始了一场属于自己的数学探险。
什么是勾股数组?
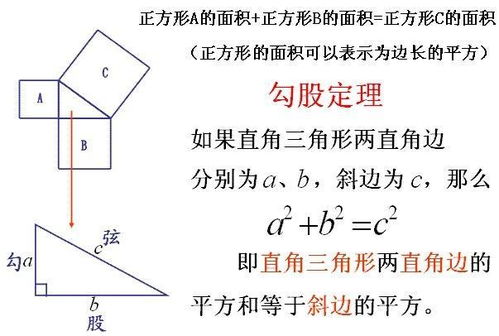
小明首先回顾了勾股定理的基本概念。勾股定理,又称毕达哥拉斯定理,描述的是直角三角形中三边的关系:若一个三角形的两条直角边分别为a和b,斜边为c,则满足公式 a² + b² = c²。而当a、b、c均为正整数时,这样的三元组就被称为勾股数组。
初识勾股数组
小明通过网络搜索,找到了一些常见的勾股数组,如(3, 4, 5)、(5, 12, 13)等。这些数字组合看似简单,但背后却蕴含着深刻的数学规律。他不禁思考,是否可以找到更多类似的数组呢?于是,他决定亲自尝试计算。
手动寻找勾股数组
为了验证自己的想法,小明列出了一张表格:
| a | b | c |
|---|---|---|
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 8 | 15 | 17 |
他按照勾股定理逐一验证这些数组是否成立,并尝试用不同的数值进行组合。虽然过程繁琐,但他乐此不疲。
深入研究与公式推导
经过几天的努力,小明逐渐发现了一些规律。例如,如果选取两个正整数m和n(m > n),可以通过以下公式生成勾股数组:a = m² - n²b = 2mnc = m² + n²
这个公式让小明兴奋不已,因为它不仅简化了寻找勾股数组的过程,还揭示了隐藏在数字背后的逻辑之美。他迫不及待地将这一发现分享给身边的朋友们。
数学的乐趣在于探索
这次探索经历让小明深刻体会到,数学并不是枯燥的公式堆砌,而是一门充满创造力和想象力的学科。每一个看似平凡的问题背后,都可能隐藏着无穷的奥秘等待我们去挖掘。
如今的小明,已经不再满足于简单的计算,而是开始涉足更复杂的数学领域。他相信,只要保持好奇心和求知欲,每个人都能在数学的世界里找到属于自己的乐趣。



发表评论 取消回复