《对数函数的图像与性质》教学反思：从困惑到突破

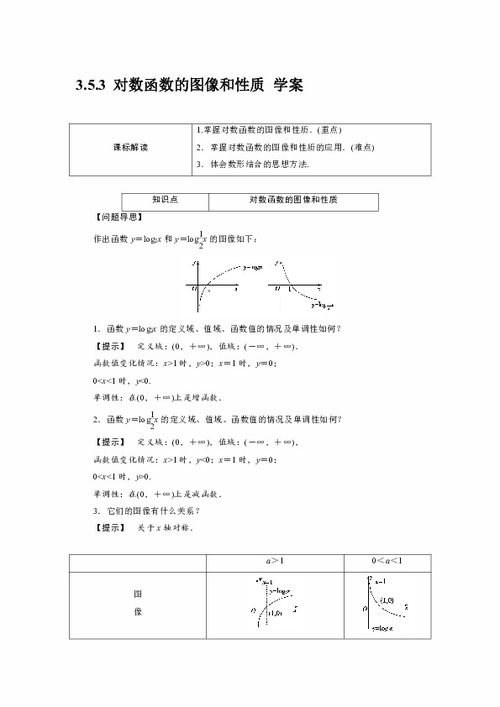
作为一名数学老师，我最近在教授《对数函数的图像与性质》这一章节时，遇到了不少挑战。这门课程不仅是高中数学的重点内容，也是学生理解后续复杂函数的基础。因此，如何让学生真正掌握对数函数的精髓，成为了我这段时间思考的核心问题。

在课堂上，我发现学生们对对数函数的理解存在明显的差异。有些学生能够快速掌握基本概念，而另一些则显得十分吃力。尤其是在画出对数函数的图像时，很多学生感到困惑，不知道如何从指数函数的图像推导出对数函数的图像。这种现象让我意识到，传统的教学方法可能已经无法满足现代学生的多样化需求。

为了更好地帮助学生理解对数函数的图像与性质，我决定尝试一些新的教学策略。首先，我调整了教学节奏，不再急于讲解复杂的公式和定理，而是从最基础的概念入手，逐步引导学生建立对对数函数的直观认识。

例如，在讲解对数函数的定义时，我引入了一个生活中的例子：假设你有一笔钱存入银行，每年的利率是固定的。如果你想知道多少年后这笔钱会翻倍，就可以用对数函数来解决这个问题。通过这个例子，学生们开始意识到对数函数并不是一个抽象的概念，而是与现实生活息息相关的工具。

接下来，我重点讲解了对数函数与指数函数之间的关系。通过对数函数的定义，我们知道，如果 y = log_a(x)，那么 a^y = x。换句话说，对数函数可以看作是指数函数的“反函数”。为了让学生更直观地理解这一点，我在黑板上画出了 y = 2^x 和 y = log_2(x) 的图像，并引导学生观察这两条曲线的对称性。通过这种方式，学生们逐渐明白了对数函数的图像实际上是指数函数图像沿直线 y = x 对称的结果。

然而，仅仅依靠黑板上的图形还不足以让学生完全掌握对数函数的性质。因此，我引入了一些互动式的教学工具，如几何画板和在线绘图软件。这些工具不仅可以让学生实时看到函数图像的变化，还能让他们亲手操作，探索不同参数对图像的影响。比如，当我们将底数 a 改变时，对数函数的图像会发生怎样的变化？通过实际操作，学生们发现，当 a > 1 时，对数函数是递增的；而当 0 < a < 1 时，对数函数则是递减的。这种动手实践的过程极大地提高了学生的学习兴趣和参与度。

除了使用技术手段，我还注重培养学生的逻辑思维能力。在讲解对数函数的性质时，我鼓励学生自己总结规律，并通过推理验证这些规律是否正确。例如，我们讨论了对数函数的定义域和值域。通过对数函数的定义，我们知道 x > 0 是对数函数的必要条件，因为负数和零没有对数。此外，我还引导学生思考，为什么对数函数的值域是全体实数？通过这些问题的探讨，学生们不仅加深了对对数函数的理解，还锻炼了自己的逻辑推理能力。

在教学过程中，我也遇到了一些挑战。例如，部分学生在理解对数函数的单调性时仍然存在困难。为了解决这个问题，我设计了一些针对性的练习题，帮助学生巩固所学知识。同时，我还组织了小组讨论，鼓励学生互相交流，分享彼此的想法。通过这种方式，学生们不仅解决了自己的疑问，还学会了如何与他人合作，共同解决问题。

经过一段时间的教学实践，我逐渐发现，对数函数的教学不仅仅是传授知识，更是培养学生思维方式的过程。通过引导学生从不同的角度去思考问题，我希望能够激发他们对数学的兴趣，培养他们的创新精神和批判性思维。在这个过程中，我也不断反思自己的教学方法，努力寻找更适合学生的教学方式。

总的来说，《对数函数的图像与性质》这一章节的教学让我收获颇丰。我不仅看到了学生们在学习中的进步，也意识到作为教师，我们需要不断适应时代的变化，探索更加有效的教学方法。未来的教学中，我将继续保持开放的心态，勇于尝试新的教学工具和方法，帮助更多学生在数学的世界里找到属于自己的乐趣和成就感。